2019中考數(shù)學(xué)一輪復(fù)習(xí)單元檢測試卷

第十六單元 二次根式

考試時間：120分鐘；滿分：150分

學(xué)校:___________姓名：___________班級：___________考號：___________

一、選擇題（本大題共10小題，每小題4分，共40分）

1．下列式子：，，，，，，中，一定是二次根式的是（　　）

A．3個B．4個C．5個D．6個

2．要使代數(shù)式有意義，則x的取值范圍是（　　）

A．x＞﹣1B．x≥﹣1C．x≠0D．x＞﹣1且x≠0

3．下列等式正確的是（　　）

A．B．C．D．

4．a、b在數(shù)軸上的位置如圖所示，那么化簡的結(jié)果是（　　）

A．a﹣bB．a+bC．b﹣aD．﹣a﹣b

5．下列各式計算正確的是（　　）

A．＝2B．÷＝C．（）2＝3D．＝﹣2

6．在將式子（m＞0）化簡時，

小明的方法是：；

小亮的方法是：；

小麗的方法是：．

則下列說法正確的是（　　）

A．小明、小亮的方法正確，小麗的方法不正確

B．小明、小麗的方法正確，小亮的方法不正確

C．小明、小亮、小麗的方法都正確

D．小明、小麗、小亮的方法都不正確

7．若a＝+、b＝﹣，則a和b互為（　　）

A．倒數(shù)B．相反數(shù)C．負(fù)倒數(shù)D．有理化因式

8．下列計算，正確的是（　　）

A．B．

C．D．

9．按如圖所示的運算程序，若輸入數(shù)字“9”，則輸出的結(jié)果是（　　）

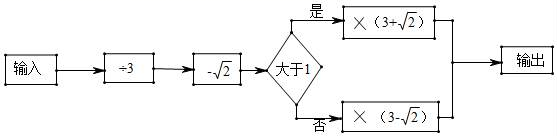
A．7B．11﹣6C．1D．11﹣3

10．如圖，在長方形ABCD中無重疊放入面積分別為16cm2和12cm2的兩張正方形紙片，則圖中空白部分的面積為（　　）cm2．

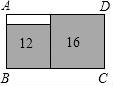
A．16﹣8B．﹣12+8C．8﹣4D．4﹣2

二、填空題（本大題共4小題，每小題5分，共20分）

11．已知等式|a﹣2018|+＝a成立，a﹣20182的值為

12．當(dāng)a＜0時，化簡：＝．

13．已知a＝2+，b＝2﹣，則a2b+ab2＝．

14．小明發(fā)明了一種用“二次根式法”來產(chǎn)生密碼的方法，如對于二次根式的計算結(jié)果是13，則在被開放數(shù)和結(jié)果時間加上數(shù)字0，就得到一個密碼“169013”，則對于二次根式，用小明的方法產(chǎn)生的這個密碼是（密碼中不寫小數(shù)點）

三、解答題（本大題共9小題，滿分90分,其中第15,16,17,18題每題8分，19,20題每題10分，21,22題每題12分，23題14分）

15．計第：

（1）（﹣）2﹣+

（2）．

16．已知|2018﹣m|+＝m，求m﹣20182的值．

17．化簡求值：已知：x＝，y＝，求（x+3）（y+3）的值．

18．設(shè)a，b，c為△ABC的三邊，化簡：

++﹣．

19．已知a＝，b＝，

（1）求ab，a+b的值；

（2）求的值．

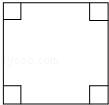
20．如圖：面積為48cm2的正方形四個角是面積為3cm2的小正方形，現(xiàn)將四個角剪掉，制作一個無蓋的長方體盒子，求這個長方體盒子的底面邊長和體積分別是多少？（精確到0.1cm，≈1.732）

21．閱讀材料：

小明在學(xué)習(xí)二次根式的化簡后，遇到了這樣一個需要化簡的式子：．該如何化簡呢？思考后，他發(fā)現(xiàn)3+2＝1+2+（）2＝（1+）2．于是＝＝1+．善于思考的小明繼續(xù)深入探索；當(dāng)a+b＝（m+n）2時（其中a，b，m，n均為正整數(shù)），則a+b＝m2+2mn+2n2．此時，a＝m2+2n2，b＝2mn，于是，＝m+n．請你仿照小明的方法探索并解決下列何題：

（1）設(shè)a，b，m，n均為正整數(shù)且＝m+n，用含m，n的式子分別表示a，b時，結(jié)果是a＝，b＝；

（2）利用（1）中的結(jié)論，選擇一組正整數(shù)填空：＝+；

（3）化簡：．

22．觀察下列各式：

＝1+﹣＝1；＝1+﹣＝1；

＝1+﹣＝1，…

請你根據(jù)以上三個等式提供的信息解答下列問題

①猜想：＝＝；

②歸納：根據(jù)你的觀察，猜想，請寫出一個用n（n為正整數(shù)）表示的等式：；

③應(yīng)用：計算．

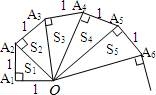
23．細(xì)心觀察圖形，認(rèn)真分析各式，然后解答問題：

OA1＝1；

OA2＝＝；S1＝×1×1＝；

OA3＝＝；S2＝××1＝；

OA4＝＝；S3＝××1＝；

（1）推算出OA10＝．

（2）若一個三角形的面積是．則它是第個三角形．

（3）用含n（n是正整數(shù)）的等式表示上述面積變化規(guī)律；

（4）求出S12+S22+S23+…+S2100的值．