2019中考數學一輪復習單元檢測試卷
第十九單元 一次函數
考試時間:120分鐘;滿分:150分
學校:___________姓名:___________班級:___________考號:___________
得 分 | 評卷人 |
|
一、選擇題(本大題共10小題,每小題4分,共40分)
1.在函數y=![]() 中,自變量x的取值范圍是( )
中,自變量x的取值范圍是( )
A.x≤﹣3B.x≥﹣3C.x<﹣3D.x>﹣3
2.變量x與y之間的關系是y=2x﹣3,當因變量y=6時,自變量x的值是( )
A.9B.15C.4.5D.1.5
3.早上,小明從家里步行去學校,出發一段時間后,小明媽媽發現小明的作業本落在家里,便帶上作業本騎車追趕,途中追上小明兩人稍作停留,媽媽騎車返回,小明繼續步行前往學校,兩人同時到達.設小明在途的時間為x,兩人之間的距離為y,則下列選項中的圖象能大致反映y與x之間關系的是( )
A.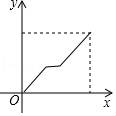 B.
B.
C.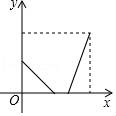 D.
D.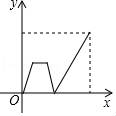
4.已知點(﹣2,y1),(﹣1,y2),(1,y3)都在直線y=﹣x上,則y1,y2,y3的大小關系是( )
A.y1>y2>y3B.y1<y2<y3C.y3>y1>y2D.y3<y1<y2
5.若函數y=kx(k≠0)的值隨自變量的增大而增大,則函數y=x+2k的圖象大致是( )
A.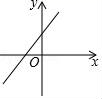 B.
B.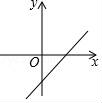
C.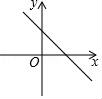 D.
D.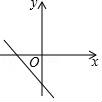
6.如圖,在平面直角坐標系中,OABC的頂點A在x軸上,定點B的坐標為(6,4),若直線經過定點(1,0),且將平行四邊形OABC分割成面積相等的兩部分,則直線的表達式( )

A.y=3x﹣2B.y=![]() x﹣
x﹣![]() C.y=x﹣1D.y=3x﹣3
C.y=x﹣1D.y=3x﹣3
7.如圖,已知一次函數y=kx+b的圖象與x軸,y軸分別交于點(2,0),點(0,3).有下列結論:①關于x的方程kx+b=0的解為x=2;②關于x的方程kx+b=3的解為x=0;③當x>2時,y<0;④當x<0時,y<3.其中正確的是( )
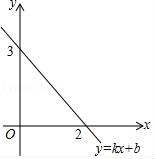
A.①②③B.①③④C.②③④D.①②④
8.速度分別為100km/h和akm/h(0<a<100)的兩車分別從相距s千米的兩地同時出發,沿同一方向勻速前行.行駛一段時間后,其中一車按原速度原路返回,直到與另一車相遇時兩車停止.在此過程中,兩車之間的距離y(km)與行駛時間t(h)之間的函數關系如圖所示.下列說法:①a=60;②b=2;③c=b+![]() ;④若s=60,則b=
;④若s=60,則b=![]() .其中說法正確的是( )
.其中說法正確的是( )
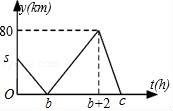
A.①②③B.②③④C.①②④D.①③④
9.如圖,已知直線l:![]() ,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;…;按此作法繼續下去,則點A4的坐標為( )
,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;…;按此作法繼續下去,則點A4的坐標為( )
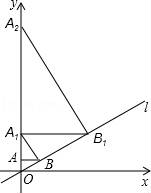
A.(0,128)B.(0,256)C.(0,512)D.(0,1024)
10.如圖,等邊三角形和正方形的邊長均為a,點B,C,D,E在同一直線上,點C與點D重合.△ABC以每秒1個單位長度的速度沿BE向右勻速運動.當點C與點E重合時停止運動.設△ABC的運動時間為t秒,△ABC與正方形DEFG重疊部分的面積為S,則下列圖象中,能表示S與t的函數關系的圖象大致是( )
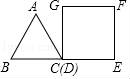
A.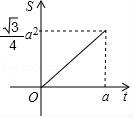 B.
B.
C.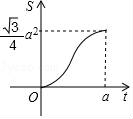 D.
D.
得 分 | 評卷人 |
|
二、填空題(本大題共4小題,每小題5分,共20分)
11.某汽車生產廠對其生產的A型汽車進行油耗試驗,試驗中汽車為勻速行駛汽在行駛過程中,油箱的余油量y(升)與行駛時間t(小時)之間的關系如下表:
t(小時) | 0 | 1 | 2 | 3 |
y(升) | 100 | 92 | 84 | 76 |
由表格中y與t的關系可知,當汽車行駛小時,油箱的余油量為0.
12.若點(a,3)在函數y=2x﹣3的圖象上,a的值是.
13.如圖,O是坐標原點,菱形OABC的頂點A的坐標為(3,4),頂點C在x軸的正半軸上,則∠AOC的角平分線所在直線的函數關系式為.
14.點A(m,n)為直線y=﹣x+4上一動點,且滿足﹣4<m<4,將O點繞點B(﹣![]() ,﹣
,﹣![]() )逆時針旋轉90°得點C,連接AC,則線段AC長度的取值范圍是.
)逆時針旋轉90°得點C,連接AC,則線段AC長度的取值范圍是.
得 分 | 評卷人 |
|
三、解答題(本大題共9小題,滿分90分,其中第15,16,17,18題每題8分,19,20題每題10分,21,22題每題12分,23題14分)
15.已知y與x+2成正比,當x=4時,y=4.
(1)求y與x之間的函數關系式;
(2)若點(a,3)在這個函數圖象上,求a的值.
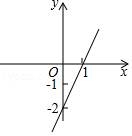
16.已知一次函數y=kx+b的圖象如圖所示
(1)求k、b的值;
(2)在平面直角坐標系內畫出函數y=bx+k的圖象;
(3)利用(2)中你所畫的圖象,寫出0<x<1時,y的取值范圍.
17.已知正比例函數y=kx圖象經過點(3,﹣6),求:
(1)這個函數的解析式;
(2)判斷點A(4,﹣2)是否在這個函數圖象上;
(3)圖象上兩點B(x1,y1)、C(x2,y2),如果x1>x2,比較y1,y2的大小.
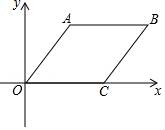
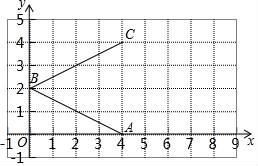
18.如圖,在平面直角坐標系中,A(4,0),B(0,2),C(4,4).已知四邊形ABCD為菱形,其中AB與BC為一組鄰邊.
(1)請在圖中作出菱形ABCD,并求出菱形ABCD的面積;
(2)過點A的直線l:y=![]() x+b與線段CD相交于點E,請在圖中作出直線l的圖象,并求出△ADE的面積.
x+b與線段CD相交于點E,請在圖中作出直線l的圖象,并求出△ADE的面積.
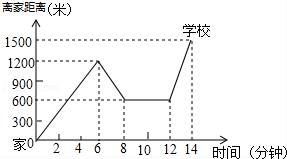
19.小明騎單車上學,當他騎了一段路時,想起要買某本書,于是又折回到剛經過的某書店,買到書后繼續去學校.以下是他本次上學所用的時間與路程的關系示意圖.
根據圖中提供的信息回答下列問題:
(1)小明家到學校的路程是米.
(2)小明在書店停留了分鐘.
(3)本次上學途中,小明一共行駛了米.一共用了分鐘.
(4)我們認為騎單車的速度超過300米/分就超過了安全限度.問:在整個上學途中哪個時間段小明的汽車速度最快,速度在安全限度內嗎?
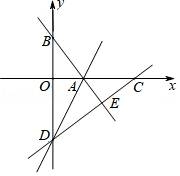
20.如圖,在平面直角坐標系xOy中,直線y=﹣![]() x+4與x軸、y軸分別交于點A、點B,點D在y軸的負半軸上,若將△DAB沿直線AD折疊,點B恰好落在x軸正半軸上的點C處.
x+4與x軸、y軸分別交于點A、點B,點D在y軸的負半軸上,若將△DAB沿直線AD折疊,點B恰好落在x軸正半軸上的點C處.
(1)求AB的長;
(2)求點C和點D的坐標;
(3)y軸上是否存在一點P,使得S△PAB=![]() S△OCD?若存在,直接寫出點P的坐標;若不存在,請說明理由.
S△OCD?若存在,直接寫出點P的坐標;若不存在,請說明理由.
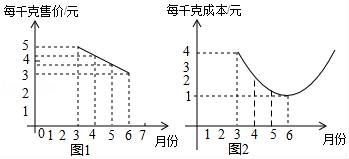
21.某種蔬菜的銷售單價y1與銷售月份x之間的關系如圖1所示,成本y2與銷售月份x之間的關系如圖2所示.
(1)已知6月份這種蔬菜的成本最低,此時出售每干克的收益是多少元?(收益=售價﹣成本)
(2)分別求出y1、y2與x之間的函數關系式;
(3)哪個月出售這種蔬菜,每千克的收益最大?說明理由.
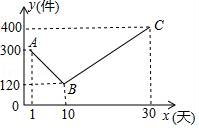
22.某公司開發處一款新的節能產品,該產品的成本價為6元/件,該產品在正式投放市場前通過代銷點進行了為期一個月(30天)的試銷售,售價為10元/件,工作人員對銷售情況進行了跟蹤記錄,并將記錄情況繪制成圖象,圖中的折線ABC表示日銷售量y(件)與銷售時間x(天)之間的函數關系.
(1)求y與x之間的函數表達式,并寫出x的取值范圍;
(2)若該節能產品的日銷售利潤為w(元),求w與x之間的函數表達式,并求出日銷售利潤不超過1040元的天數共有多少天?
(3)若5≤x≤17,直接寫出第幾天的日銷售利潤最大,最大日銷售利潤是多少元(不用說理)
23.閱讀下列兩段材料,回答問題:
材料一:點A(x1,y1),B(x2,y2)的中點坐標為(![]() ,
,![]() ).例如,點(1,5),(3,﹣1)的中點坐標為(
).例如,點(1,5),(3,﹣1)的中點坐標為(![]() ,
,![]() ),即(2,2).
),即(2,2).
材料二:如圖1,正比例函數l1:y=k1x和l2:y=k2x的圖象相互垂直,分別在l1和l2上取點A,B,使得AO=BO.分別過點A,B作x軸的垂線,垂足分別為點C,D.顯然,△AOC≌△OBD.設OC=BD=a,AC=OD=b,則A(﹣a,b),B(b,a).于是k1=﹣![]() ,k2=
,k2=![]() ,所以k1?k2的值為一個常數.一般地,一次函數y=k1x+b1,y=k2x+b2可分別由正比例函數l1,l2平移得到.
,所以k1?k2的值為一個常數.一般地,一次函數y=k1x+b1,y=k2x+b2可分別由正比例函數l1,l2平移得到.
所以,我們經過探索得到的結論是:任意兩個一次函數y=k1x+b1,y=k2x+b2的圖象相互垂直,則k1?k2的值為一個常數.
(1)在材料二中,k1?k2=(寫出這個常數具體的值);
(2)如圖2,在矩形OBAC中A(4,2),點D是OA中點,用兩段材料的結論,求點D的坐標和OA的垂直平分線l的解析式;
(3)若點C′與點C關于OA對稱,用兩段材料的結論,求點C′的坐標.