2019中考數學一輪復習單元檢測試卷
第十七單元 勾股定理
考試時間:120分鐘;滿分:150分
學校:___________姓名:___________班級:___________考號:___________
得 分 | 評卷人 |
|
一、選擇題(本大題共10小題,每小題4分,共40分)
1.下列各組數中,是勾股數的是( )
A.1、2、3B.3、4、5C.12、15、18D.1、![]() 、3
、3
2.如果3,a,5是勾股數,則a的值是( )
A.4B.![]() C.4或
C.4或![]() D.4或34
D.4或34
3.如圖,在正方形網格中,每個正方形的邊長為1,則在△ABC中,邊長為無理數的邊數是( )
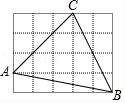
A.0B.1C.2D.3
4.在△ABC中,∠B=90°,若BC=3,AC=5,則AB等于( )
A.2B.3C.4D.![]()
5.如圖,在Rt△ABC中,∠C=90°,分別以各邊為直徑作半圓,圖中陰影部分在數學史上稱為“希波克拉底月牙”,當AC=4,BC=2時,則陰影部分的面積為( )
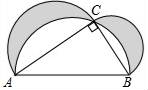
A.4B.4πC.8πD.8
6.如圖,數軸上點A對應的數是0,點B對應的數是1,BC⊥AB,垂足為B,且BC=2,以A為圓心,AC為半徑畫弧,交數軸于點D,則點D表示的數為( )
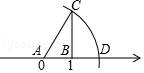
A.2.2B.![]() C.
C.![]() D.
D.![]()
7.我國是最早了解勾股定理的國家之一.下面四幅圖中,不能證明勾股定理的是( )
A.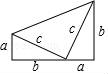 B.
B.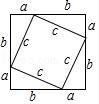
C.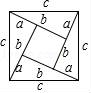 D.
D.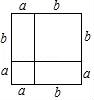
8.已知△ABC的三邊為a,b,c,下列條件能判定△ABC為直角三角形的是( )
A.a:b:c=1:1:![]() B.a:b:c=1:1:
B.a:b:c=1:1:![]()
C.a:b:c=2:2:3D.a:b:c=![]() :2:
:2:![]()
9.“折竹抵地”問題源自《九章算術》中,即:今有竹高一丈,末折抵地,去本四尺,問折者高幾何?意思是:一根竹子,原高一丈,一陣風將竹子折斷,其竹梢恰好抵地,抵地處離竹子底部4尺遠(如圖),則折斷后的竹子高度為多少尺?(1丈=10尺)( )
A.3B.5C.4.2D.4
10.在《算法統宗》中有一道“蕩秋千”的問題:“平地秋千未起,踏板一尺離地.送行二步與人齊,五尺人高曾記.仕女佳人爭蹴,終朝笑語歡嬉.良工高士素好奇,算出索長有幾?”譯文:“有一架秋千,當它靜止時,踏板離地1尺,將它往前推送10尺(水平距離)時,秋千的踏板就和人一樣高,這個人的身高為5尺,秋千的繩索始終拉得很直,試問繩索有多長?”.設這個人的身高是5尺,秋千的繩索始終拉的很直,則繩索長為( )
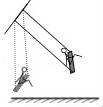
A.12.5尺B.13.5尺C.14.5尺D.15.5尺
得 分 | 評卷人 |
|
二、填空題(本大題共4小題,每小題5分,共20分)
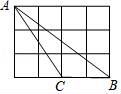
11.如圖,長方形網格中每個小正方形的邊長是1,△ABC是格點三角形(頂點都在格點上),則點C到AB的距離為.
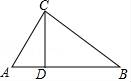
12.若CD是△ABC的高,AB=10,AC=6,BC=8,則CD的長為.
13.有兩根木棒,分別長6cm、5cm,要再在7cm的木棒上取一段,用這三根木棒為邊做成直角三角形,這第三根木棒要取的長度是.
14.勾股定理a2+b2=c2本身就是一個關于a,b,c的方程,滿足這個方程的正整數解(a,b,c)通常叫做勾股數組.畢達哥拉斯學派提出了一個構造勾股數組的公式,根據該公式可以構造出如下勾股數組:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股數組可以發現,4=1×(3+1),12=2×(5+1),24=3×(7+1),…分析上面規律,第5個勾股數組為.

得 分 | 評卷人 |
|
三、解答題(本大題共9小題,滿分90分,其中第15,16,17,18題每題8分,19,20題每題10分,21,22題每題12分,23題14分)
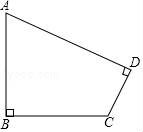
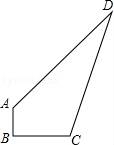
15.如圖,在四邊形ABCD中,∠B=∠D=90°,AB=BC=2,CD=1,求AD的長.
16.某廣場內有一塊空地ABCD如圖所示,現計劃在空地上種草皮,經測量,∠B=90°,AB=6m,BC=8m,CD=26m,AD=24m.求四邊形ABCD空地的面積.
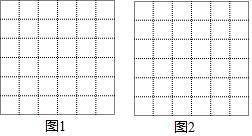
17.如圖,正方形網格中每個小正方形邊長都是1,小正方形的頂點稱為格點,在正方形網格中分別畫出下列圖形:
(1)在網格中畫出長為![]() 的線段AB.
的線段AB.
(2)在網格中畫出一個腰長為![]() 、面積為3的等腰△DEF.
、面積為3的等腰△DEF.
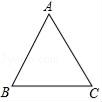
18.如果三角形有一邊上的中線恰好等于這邊的長,那么我們稱這個三角形為“美麗三角形”,
(1)如圖△ABC中,AB=AC=![]() ,BC=2,求證:△ABC是“美麗三角形”;
,BC=2,求證:△ABC是“美麗三角形”;
(2)在Rt△ABC中,∠C=90°,AC=2![]() ,若△ABC是“美麗三角形”,求BC的長.
,若△ABC是“美麗三角形”,求BC的長.
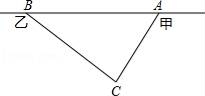
19.在甲村至乙村的公路有一塊山地正在開發,現有一C處需要爆破.已知點C與公路上的停靠站A的距離為300米,與公路上的另一停靠站B的距離為400米,且CA⊥CB,如圖所示.為了安全起見,爆破點C周圍半徑250米范圍內不得進入,問在進行爆破時,公路AB段是否有危險而需要暫時封鎖?請通過計算進行說明.
20.如果a,b,c為正整數,且滿足a2+b2=c2,那么,a、b、c叫做一組勾股數.
(1)請你根據勾股數的意思,說明3、4、5是一組勾股數;
(2)寫出一組不同于3、4、5的勾股數;
(3)如果m表示大于1的整數,且a=4m,b=4m2﹣1,c=4m2+1,請你根據勾股數的定義,說明a、b、c為勾股數.
21.[問題情境]
勾股定理是一條古老的數學定理,它有很多種證明方法,我國漢代數學家趙爽根據弦圖,利用面積法進行證明,著名數學家華羅庚曾提出把“數形關系”(勾股定理)帶到其他星球,作為地球人與其他星球“人”進行第一次“談話”的語言.
[定理表述]
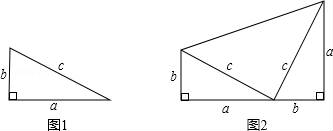
請你根據圖1中的直角三角形,寫出勾股定理內容;
[嘗試證明]
以圖1中的直角三角形為基礎,可以構造出以a、b為底,以a+b為高的直角梯形(如圖2),請你利用圖2,驗證勾股定理.
22.閱讀下列一段文字,然后回答下列問題.
已知在平面內有兩點P1(x1,y1)、P2(x2,y2),其兩點間的距離P1P2=![]() ,同時,當兩點所在的直線在坐標軸或平行于坐標軸或垂直于坐標軸時,兩點間距離公式可化簡為|x2﹣x1|或|y2﹣y1|.
,同時,當兩點所在的直線在坐標軸或平行于坐標軸或垂直于坐標軸時,兩點間距離公式可化簡為|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),試求A、B兩點間的距離;
(2)已知M、N在平行于y軸的直線上,點M的縱坐標為4,點N的縱坐標為﹣1,試求M、N兩點的距離為;
(3)已知一個三角形各頂點坐標為D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形狀嗎?說明理由.
(4)在(3)的條件下,平面直角坐標系中,在x軸上找一點P,使PD+PF的長度最短,求出點P的坐標及PD+PF的最短長度.
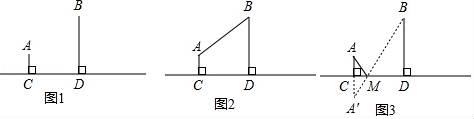
23.如圖1,A村和B村在一條大河CD的同側,它們到河岸的距離AC、BD分別為1千米和4千米,又知道CD的長為4千米.
(1)現要在河岸CD上建一水廠向兩村輸送自來水.有兩種方案備選
方案1:水廠建在C點,修自來水管道到A村,再到B村(即AC+AB).(如圖2)
方案2:作A點關于直線CD的對稱點A',連接A'B交CD于M點,水廠建在M點處,分別向兩村修管道AM和BM.(即AM+BM)(如圖3)
從節約建設資金方面考慮,將選擇管道總長度較短的方案進行施工,請利用已有條件分別進行計算,判斷哪種方案更合適.
(2)有一艘快艇Q從這條河中駛過,當快艇Q在CD中間,DQ為多少時?△ABQ為等腰三角形?






