2018年普通高等學校招生全國統一考試
文科數學
注意事項:
1.答卷前,考生務必將自己的姓名和準考證號填寫在答題卡上。
2.回答選擇題時,選出每小題答案后,用鉛筆把答題卡對應題目的答案標號涂黑。如需改動,用橡皮擦干凈后,再選涂其它答案標號。回答非選擇題時,將答案寫在答題卡上。寫在本試卷上無效。
3.考試結束后,將本試卷和答題卡一并交回。
一、選擇題:本題共12小題,每小題5分,共60分。在每小題給出的四個選項中,只有一項是符合題目要求的。
1.已知集合![]() ,
,![]() ,則
,則![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.設![]() ,則
,則![]()
A.0B.![]() C.
C.![]() D.
D.![]()
3.某地區經過一年的新農村建設,農村的經濟收入增加了一倍.實現翻番.為更好地了解該地區農村的經濟收入變化情況,統計了該地區新農村建設前后農村的經濟收入構成比例.得到如下餅圖:
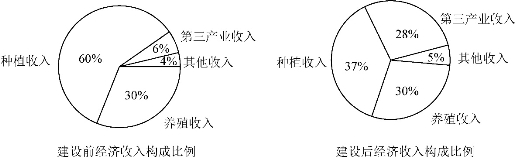
則下面結論中不正確的是
A.新農村建設后,種植收入減少
B.新農村建設后,其他收入增加了一倍以上
C.新農村建設后,養殖收入增加了一倍
D.新農村建設后,養殖收入與第三產業收入的總和超過了經濟收入的一半
4.已知橢圓![]() :
:![]() 的一個焦點為
的一個焦點為![]() ,則
,則![]() 的離心率為
的離心率為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知圓柱的上、下底面的中心分別為![]() ,
,![]() ,過直線
,過直線![]() 的平面截該圓柱所得的截面是面積為8的正方形,則該圓柱的表面積為
的平面截該圓柱所得的截面是面積為8的正方形,則該圓柱的表面積為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.設函數![]() .若
.若![]() 為奇函數,則曲線
為奇函數,則曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在△![]() 中,
中,![]() 為
為![]() 邊上的中線,
邊上的中線,![]() 為
為![]() 的中點,則
的中點,則![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.已知函數![]() ,則
,則
A.![]() 的最小正周期為π,最大值為3
的最小正周期為π,最大值為3
B.![]() 的最小正周期為π,最大值為4
的最小正周期為π,最大值為4
C.![]() 的最小正周期為
的最小正周期為![]() ,最大值為3
,最大值為3
D.![]() 的最小正周期為
的最小正周期為![]() ,最大值為4
,最大值為4
9.某圓柱的高為2,底面周長為16,其三視圖如右圖.圓柱表面上的點![]() 在正視圖上的對應點為
在正視圖上的對應點為![]() ,圓柱表面上的點
,圓柱表面上的點![]() 在左視圖上的對應點為
在左視圖上的對應點為![]() ,則在此圓柱側面上,從
,則在此圓柱側面上,從![]() 到
到![]() 的路徑中,最短路徑的長度為
的路徑中,最短路徑的長度為
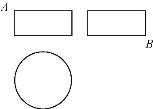
A.![]() B.
B.![]()
C.![]() D.2
D.2
10.在長方體![]() 中,
中,![]() ,
,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,則該長方體的體積為
,則該長方體的體積為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知角![]() 的頂點為坐標原點,始邊與
的頂點為坐標原點,始邊與![]() 軸的非負半軸重合,終邊上有兩點
軸的非負半軸重合,終邊上有兩點![]() ,
,![]() ,且
,且
![]() ,則
,則![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.設函數![]() ,則滿足
,則滿足![]() 的x的取值范圍是
的x的取值范圍是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空題:本題共4小題,每小題5分,共20分。
13.已知函數![]() ,若
,若![]() ,則
,則![]() ________.
________.
14.若![]() 滿足約束條件
滿足約束條件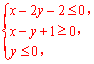 則
則![]() 的最大值為________.
的最大值為________.
15.直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,則
兩點,則![]() ________.
________.
16.△![]() 的內角
的內角![]() 的對邊分別為
的對邊分別為![]() ,已知
,已知![]() ,
,![]() ,則△
,則△![]() 的面積為________.
的面積為________.
三、解答題:共70分。解答應寫出文字說明、證明過程或演算步驟。第17~21題為必考題,每個試題考生都必須作答。第22、23題為選考題,考生根據要求作答。
(一)必考題:共60分。
17.(12分)
已知數列![]() 滿足
滿足![]() ,
,![]() ,設
,設![]() .
.
(1)求![]() ;
;
(2)判斷數列![]() 是否為等比數列,并說明理由;
是否為等比數列,并說明理由;
(3)求![]() 的通項公式.
的通項公式.
18.(12分)
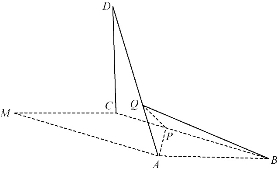
如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為折痕將△
為折痕將△![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且
的位置,且![]() .
.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)![]() 為線段
為線段![]() 上一點,
上一點,![]() 為線段
為線段![]() 上一點,且
上一點,且![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
19.(12分)
某家庭記錄了未使用節水龍頭50天的日用水量數據(單位:m3)和使用了節水龍頭50天的日用水量數據,得到頻數分布表如下:
未使用節水龍頭50天的日用水量頻數分布表
日用水量 |
|
|
|
|
|
|
|
頻數 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節水龍頭50天的日用水量頻數分布表
日用水量 |
|
|
|
|
|
|
頻數 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答題卡上作出使用了節水龍頭50天的日用水量數據的頻率分布直方圖:
(2)估計該家庭使用節水龍頭后,日用水量小于0.35m3的概率;
(3)估計該家庭使用節水龍頭后,一年能節省多少水?(一年按365天計算,同一組中的數據以這組數據所在區間中點的值作代表.)
20.(12分)
設拋物線![]() ,點
,點![]() ,
,![]() ,過點
,過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)當![]() 與
與![]() 軸垂直時,求直線
軸垂直時,求直線![]() 的方程;
的方程;
(2)證明:![]() .
.
21.(12分)
已知函數![]() .
.
(1)設![]() 是
是![]() 的極值點,求
的極值點,求![]() ,并求
,并求![]() 的單調區間;
的單調區間;
(2)證明:當![]() 時,
時,![]() .
.
(二)選考題:共10分。請考生在第22、23題中任選一題作答。如果多做,則按所做的第一題計分。
22.[選修4—4:坐標系與參數方程](10分)
在直角坐標系![]() 中,曲線
中,曲線![]() 的方程為
的方程為![]() .以坐標原點為極點,
.以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 有且僅有三個公共點,求
有且僅有三個公共點,求![]() 的方程.
的方程.
23.[選修4—5:不等式選講](10分)
已知![]() .
.
(1)當![]() 時,求不等式
時,求不等式![]() 的解集;
的解集;
(2)若![]() 時不等式
時不等式![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.






