2019年全國統(tǒng)一高考數(shù)學(xué)試卷(理科)(新課標(biāo)Ⅰ)
一、選擇題:本題共12小題,每小題5分,共60分。在每小題給出的四個選項中,只有一項是符合題目要求的。
1.(5分)已知集合M={x|﹣4<x<2},N={x|x2﹣x﹣6<0},則M∩N=( )
A.{x|﹣4<x<3}B.{x|﹣4<x<﹣2}C.{x|﹣2<x<2}D.{x|2<x<3}
2.(5分)設(shè)復(fù)數(shù)z滿足|z﹣i|=1,z在復(fù)平面內(nèi)對應(yīng)的點為(x,y),則( )
A.(x+1)2+y2=1B.(x﹣1)2+y2=1
C.x2+(y﹣1)2=1D.x2+(y+1)2=1
3.(5分)已知a=log20.2,b=20.2,c=0.20.3,則( )
 A.a<b<cB.a<c<bC.c<a<bD.b<c<a
A.a<b<cB.a<c<bC.c<a<bD.b<c<a
4.(5分)古希臘時期,人們認(rèn)為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是![]() (
(![]() 0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是
0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是![]() .若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26cm,則其身高可能是( )
.若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26cm,則其身高可能是( )
A.165cmB.175cmC.185cmD.190cm
5.(5分)函數(shù)f(x)![]() 在[﹣π,π]的圖象大致為( )
在[﹣π,π]的圖象大致為( )
A.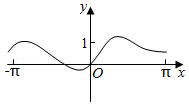 B.
B.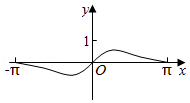
C.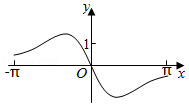 D.
D.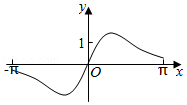
 6.(5分)我國古代典籍《周易》用“卦”描述萬物的變化.每一“重卦”由從下到上排列的6個爻組成,爻分為陽爻“
6.(5分)我國古代典籍《周易》用“卦”描述萬物的變化.每一“重卦”由從下到上排列的6個爻組成,爻分為陽爻“![]() ”和陰爻“
”和陰爻“![]() ”,如圖就是一重卦.在所有重卦中隨機取一重卦,則該重卦恰有3個陽爻的概率是( )
”,如圖就是一重卦.在所有重卦中隨機取一重卦,則該重卦恰有3個陽爻的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(5分)已知非零向量![]() ,
,![]() 滿足|
滿足|![]() |=2|
|=2|![]() |,且(
|,且(![]() )⊥
)⊥![]() ,則
,則![]() 與
與![]() 的夾角為( )
的夾角為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
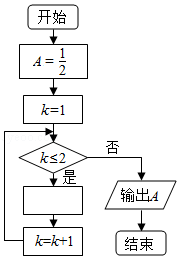 8.(5分)如圖是求
8.(5分)如圖是求![]() 的程序框圖,圖中空白框中應(yīng)填入( )
的程序框圖,圖中空白框中應(yīng)填入( )
A.A![]() B.A=2
B.A=2![]()
C.A![]() D.A=1
D.A=1![]()
9.(5分)記Sn為等差數(shù)列{an}的前n項和.已知S4=0,a5=5,則( )
A.an=2n﹣5B.an=3n﹣10
C.Sn=2n2﹣8nD.Sn![]() n2﹣2n
n2﹣2n
10.(5分)已知橢圓C的焦點為F1(﹣1,0),F2(1,0),過F2的直線與C交于A,B兩點.若|AF2|=2|F2B|,|AB|=|BF1|,則C的方程為( )
A.![]() y2=1B.
y2=1B.![]() 1C.
1C.![]() 1D.
1D.![]() 1
1
11.(5分)關(guān)于函數(shù)f(x)=sin|x|+|sinx|有下述四個結(jié)論:
①f(x)是偶函數(shù)②f(x)在區(qū)間(![]() ,π)單調(diào)遞增
,π)單調(diào)遞增
③f(x)在[﹣π,π]有4個零點④f(x)的最大值為2
其中所有正確結(jié)論的編號是( )
A.①②④B.②④C.①④D.①③
12.(5分)已知三棱錐P﹣ABC的四個頂點在球O的球面上,PA=PB=PC,△ABC是邊長為2的正三角形,E,F分別是PA,AB的中點,∠CEF=90°,則球O的體積為( )
A.8![]() πB.4
πB.4![]() πC.2
πC.2![]() πD.
πD.![]() π
π
二、填空題:本題共4小題,每小題5分,共20分。
13.(5分)曲線y=3(x2+x)ex在點(0,0)處的切線方程為.
14.(5分)記Sn為等比數(shù)列{an}的前n項和.若a1![]() ,a42=a6,則S5=.
,a42=a6,則S5=.
15.(5分)甲、乙兩隊進行籃球決賽,采取七場四勝制(當(dāng)一隊贏得四場勝利時,該隊獲勝,決賽結(jié)束).根據(jù)前期比賽成績,甲隊的主客場安排依次為“主主客客主客主”.設(shè)甲隊主場取勝的概率為0.6,客場取勝的概率為0.5,且各場比賽結(jié)果相互獨立,則甲隊以4:1獲勝的概率是.
16.(5分)已知雙曲線C:![]() 1(a>0,b>0)的左、右焦點分別為F1,F2,過F1的直線與C的兩條漸近線分別交于A,B兩點.若
1(a>0,b>0)的左、右焦點分別為F1,F2,過F1的直線與C的兩條漸近線分別交于A,B兩點.若![]() ,
,![]() ?
?![]() 0,則C的離心率為.
0,則C的離心率為.
三、解答題:共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟。第17~21題為必考題,每個試題考生都必須作答。第22、23題為選考題,考生根據(jù)要求作答。(一)必考題:共60分。
17.(12分)△ABC的內(nèi)角A,B,C的對邊分別為a,b,c.設(shè)(sinB﹣sinC)2=sin2A﹣sinBsinC.
(1)求A;
 (2)若
(2)若![]() a+b=2c,求sinC.
a+b=2c,求sinC.
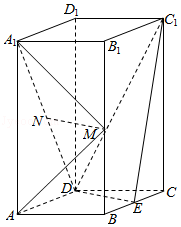
18.(12分)如圖,直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分別是BC,BB1,A1D的中點.
(1)證明:MN∥平面C1DE;
(2)求二面角A﹣MA1﹣N的正弦值.
19.(12分)已知拋物線C:y2=3x的焦點為F,斜率為![]() 的直線l與C的交點為A,B,與x軸的交點為P.
的直線l與C的交點為A,B,與x軸的交點為P.
(1)若|AF|+|BF|=4,求l的方程;
(2)若![]() 3
3![]() ,求|AB|.
,求|AB|.
20.(12分)已知函數(shù)f(x)=sinx﹣ln(1+x),f′(x)為f(x)的導(dǎo)數(shù).證明:
(1)f′(x)在區(qū)間(﹣1,![]() )存在唯一極大值點;
)存在唯一極大值點;
(2)f(x)有且僅有2個零點.
21.(12分)為治療某種疾病,研制了甲、乙兩種新藥,希望知道哪種新藥更有效,為此進行動物試驗.試驗方案如下:每一輪選取兩只白鼠對藥效進行對比試驗.對于兩只白鼠,隨機選一只施以甲藥,另一只施以乙藥.一輪的治療結(jié)果得出后,再安排下一輪試驗.當(dāng)其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時,就停止試驗,并認(rèn)為治愈只數(shù)多的藥更有效.為了方便描述問題,約定:對于每輪試驗,若施以甲藥的白鼠治愈且施以乙藥的白鼠未治愈則甲藥得1分,乙藥得﹣1分;若施以乙藥的白鼠治愈且施以甲藥的白鼠未治愈則乙藥得1分,甲藥得﹣1分;若都治愈或都未治愈則兩種藥均得0分.甲、乙兩種藥的治愈率分別記為α和β,一輪試驗中甲藥的得分記為X.
(1)求X的分布列;
(2)若甲藥、乙藥在試驗開始時都賦予4分,pi(i=0,1,…,8)表示“甲藥的累計得分為i時,最終認(rèn)為甲藥比乙藥更有效”的概率,則p0=0,p8=1,pi=api﹣1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=﹣1),b=P(X=0),c=P(X=1).假設(shè)α=0.5,β=0.8.
(i)證明:{pi+1﹣pi}(i=0,1,2,…,7)為等比數(shù)列;
(ii)求p4,并根據(jù)p4的值解釋這種試驗方案的合理性.
(二)選考題:共10分。請考生在第22、23題中任選一題作答。如果多做,則按所做的第一題計分。[選修4-4:坐標(biāo)系與參數(shù)方程](10分)
22.(10分)在直角坐標(biāo)系xOy中,曲線C的參數(shù)方程為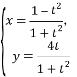 (t為參數(shù)).以坐標(biāo)原點O為極點,x軸的正半軸為極軸建立極坐標(biāo)系,直線l的極坐標(biāo)方程為2ρcosθ
(t為參數(shù)).以坐標(biāo)原點O為極點,x軸的正半軸為極軸建立極坐標(biāo)系,直線l的極坐標(biāo)方程為2ρcosθ![]() ρsinθ+11=0.
ρsinθ+11=0.
(1)求C和l的直角坐標(biāo)方程;
(2)求C上的點到l距離的最小值.
[選修4-5:不等式選講](10分)
23.已知a,b,c為正數(shù),且滿足abc=1.證明:
(1)![]() a2+b2+c2;
a2+b2+c2;
(2)(a+b)3+(b+c)3+(c+a)3≥24.
更多高中數(shù)學(xué)試卷
- 2025年春考必備:2024年上海市春季高考數(shù)學(xué)試卷.docx
- 2024年上海市高考數(shù)學(xué)試卷.doc
- 北京2024高考數(shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國統(tǒng)一考試文科數(shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國統(tǒng)一考試數(shù)學(xué)(文)(北京卷).docx
- 2018年普通高等學(xué)校招生全國統(tǒng)一考試(江蘇卷)數(shù)學(xué)Ⅰ.docx
- 2018年普通高等學(xué)校招生全國(Ⅱ)統(tǒng)一考試文科數(shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國統(tǒng)一考試數(shù) 學(xué)(理)(北京卷).docx
- 2018年普通高等學(xué)校招生全國統(tǒng)一考試?yán)砜茢?shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國(Ⅱ)統(tǒng)一考試?yán)砜茢?shù)學(xué).docx






