- 當(dāng)前位置:
- 好師來(lái)首頁(yè)
- 學(xué)科首頁(yè)
- 資源預(yù)覽
2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試(江蘇卷)數(shù)學(xué)Ⅰ
參考公式:
錐體的體積![]() ,其中
,其中![]() 是錐體的底面積,
是錐體的底面積,![]() 是錐體的高.
是錐體的高.
一、填空題:本大題共14小題,每小題5分,共計(jì)70分.請(qǐng)把答案填寫(xiě)在答題卡相應(yīng)位置上.
1.已知集合![]() ,
,![]() ,那么
,那么![]() .
.
2.若復(fù)數(shù)![]() 滿足
滿足![]() ,其中i是虛數(shù)單位,則
,其中i是虛數(shù)單位,則![]() 的實(shí)部為.
的實(shí)部為.
3.已知5位裁判給某運(yùn)動(dòng)員打出的分?jǐn)?shù)的莖葉圖如圖所示,那么這5位裁判打出的分?jǐn)?shù)的平均數(shù)為.

4.一個(gè)算法的偽代碼如圖所示,執(zhí)行此算法,最后輸出的S的值為.

5.函數(shù)![]() 的定義域?yàn)?/span>.
的定義域?yàn)?/span>.
6.某興趣小組有2名男生和3名女生,現(xiàn)從中任選2名學(xué)生去參加活動(dòng),則恰好選中2名女生的概率為
.
7.已知函數(shù)![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對(duì)稱,則
對(duì)稱,則![]() 的值是.
的值是.
8.在平面直角坐標(biāo)系![]() 中,若雙曲線
中,若雙曲線![]() 的右焦點(diǎn)
的右焦點(diǎn)![]() 到一條漸近線的距離為
到一條漸近線的距離為![]() ,則其離心率的值是.
,則其離心率的值是.
9.函數(shù)![]() 滿足
滿足![]() ,且在區(qū)間
,且在區(qū)間![]() 上,
上,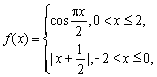 則
則![]() 的值為
的值為
.
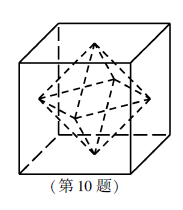
10.如圖所示,正方體的棱長(zhǎng)為2,以其所有面的中心為頂點(diǎn)的多面體的體積為.
11.若函數(shù)![]() 在
在![]() 內(nèi)有且只有一個(gè)零點(diǎn),則
內(nèi)有且只有一個(gè)零點(diǎn),則![]() 在
在![]() 上的最大值與最小值的和為.
上的最大值與最小值的和為.
12.在平面直角坐標(biāo)系![]() 中,A為直線
中,A為直線![]() 上在第一象限內(nèi)的點(diǎn),
上在第一象限內(nèi)的點(diǎn),![]() ,以AB為直徑的圓C與直線l交于另一點(diǎn)D.若
,以AB為直徑的圓C與直線l交于另一點(diǎn)D.若![]() ,則點(diǎn)A的橫坐標(biāo)為.
,則點(diǎn)A的橫坐標(biāo)為.
13.在![]() 中,角
中,角![]() 所對(duì)的邊分別為
所對(duì)的邊分別為![]() ,
,![]() ,
,![]() 的平分線交
的平分線交![]() 于點(diǎn)D,且
于點(diǎn)D,且![]() ,則
,則![]() 的最小值為.
的最小值為.
14.已知集合![]() ,
,![]() .將
.將![]() 的所有元素從小到大依次排列構(gòu)成一個(gè)數(shù)列
的所有元素從小到大依次排列構(gòu)成一個(gè)數(shù)列![]() .記
.記![]() 為數(shù)列
為數(shù)列![]() 的前n項(xiàng)和,則使得
的前n項(xiàng)和,則使得![]() 成立的n的最小值為.
成立的n的最小值為.
 二、解答題:本大題共6小題,共計(jì)90分.請(qǐng)?jiān)?/span>答題卡指定區(qū)域內(nèi)作答,解答時(shí)應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.
二、解答題:本大題共6小題,共計(jì)90分.請(qǐng)?jiān)?/span>答題卡指定區(qū)域內(nèi)作答,解答時(shí)應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.
15.(本小題滿分14分)
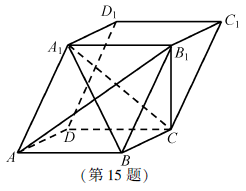
在平行六面體![]() 中,
中,![]() .
.
求證:(1)![]() ;
;
(2)![]() .
.
16.(本小題滿分14分)
已知![]() 為銳角,
為銳角,![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
17.(本小題滿分14分)
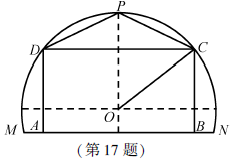 某農(nóng)場(chǎng)有一塊農(nóng)田,如圖所示,它的邊界由圓O的一段圓弧
某農(nóng)場(chǎng)有一塊農(nóng)田,如圖所示,它的邊界由圓O的一段圓弧![]() (P為此圓弧的中點(diǎn))和線段MN構(gòu)成.已知圓O的半徑為40米,點(diǎn)P到MN的距離為50米.現(xiàn)規(guī)劃在此農(nóng)田上修建兩個(gè)溫室大棚,大棚Ⅰ內(nèi)的地塊形狀為矩形ABCD,大棚Ⅱ內(nèi)的地塊形狀為
(P為此圓弧的中點(diǎn))和線段MN構(gòu)成.已知圓O的半徑為40米,點(diǎn)P到MN的距離為50米.現(xiàn)規(guī)劃在此農(nóng)田上修建兩個(gè)溫室大棚,大棚Ⅰ內(nèi)的地塊形狀為矩形ABCD,大棚Ⅱ內(nèi)的地塊形狀為![]() ,要求
,要求![]() 均在線段
均在線段![]() 上,
上,![]() 均在圓弧上.設(shè)OC與MN所成的角為
均在圓弧上.設(shè)OC與MN所成的角為![]() .
.
(1)用![]() 分別表示矩形
分別表示矩形![]() 和
和![]() 的面積,并確定
的面積,并確定![]() 的取值范圍;
的取值范圍;
(2)若大棚Ⅰ內(nèi)種植甲種蔬菜,大棚Ⅱ內(nèi)種植乙種蔬菜,且甲、乙兩種蔬菜的單位面積年產(chǎn)值之比為![]() .求當(dāng)
.求當(dāng)![]() 為何值時(shí),能使甲、乙兩種蔬菜的年總產(chǎn)值最大.
為何值時(shí),能使甲、乙兩種蔬菜的年總產(chǎn)值最大.
 18.(本小題滿分16分)
18.(本小題滿分16分)
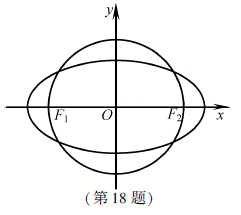
如圖,在平面直角坐標(biāo)系![]() 中,橢圓C過(guò)點(diǎn)
中,橢圓C過(guò)點(diǎn)![]() ,焦點(diǎn)
,焦點(diǎn)![]() ,圓O的直徑為
,圓O的直徑為![]() .
.
(1)求橢圓C及圓O的方程;
(2)設(shè)直線l與圓O相切于第一象限內(nèi)的點(diǎn)P.
①若直線l與橢圓C有且只有一個(gè)公共點(diǎn),求點(diǎn)P的坐標(biāo);
②直線l與橢圓C交于![]() 兩點(diǎn).若
兩點(diǎn).若![]() 的面積為
的面積為![]() ,
,
求直線l的方程.
19.(本小題滿分16分)
記![]() 分別為函數(shù)
分別為函數(shù)![]() 的導(dǎo)函數(shù).若存在
的導(dǎo)函數(shù).若存在![]() ,滿足
,滿足![]() 且
且![]() ,則稱
,則稱![]() 為函數(shù)
為函數(shù)![]() 與
與![]() 的一個(gè)“S點(diǎn)”.
的一個(gè)“S點(diǎn)”.
(1)證明:函數(shù)![]() 與
與![]() 不存在“S點(diǎn)”;
不存在“S點(diǎn)”;
(2)若函數(shù)![]() 與
與![]() 存在“S點(diǎn)”,求實(shí)數(shù)a的值;
存在“S點(diǎn)”,求實(shí)數(shù)a的值;
(3)已知函數(shù)![]() ,
,![]() .對(duì)任意
.對(duì)任意![]() ,判斷是否存在
,判斷是否存在![]() ,使函數(shù)
,使函數(shù)![]() 與
與![]() 在區(qū)間
在區(qū)間![]() 內(nèi)存在“S點(diǎn)”,并說(shuō)明理由.
內(nèi)存在“S點(diǎn)”,并說(shuō)明理由.
20.(本小題滿分16分)
設(shè)![]() 是首項(xiàng)為
是首項(xiàng)為![]() ,公差為d的等差數(shù)列,
,公差為d的等差數(shù)列,![]() 是首項(xiàng)為
是首項(xiàng)為![]() ,公比為q的等比數(shù)列.
,公比為q的等比數(shù)列.
(1)設(shè)![]() ,若
,若![]() 對(duì)
對(duì)![]() 均成立,求d的取值范圍;
均成立,求d的取值范圍;
(2)若![]() ,證明:存在
,證明:存在![]() ,使得
,使得![]() 對(duì)
對(duì)![]() 均成立,并求
均成立,并求![]() 的取值范圍(用
的取值范圍(用![]() 表示).
表示).
更多高中數(shù)學(xué)試卷
- 2025年春考必備:2024年上海市春季高考數(shù)學(xué)試卷.docx
- 2024年上海市高考數(shù)學(xué)試卷.doc
- 北京2024高考數(shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試文科數(shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試數(shù)學(xué)(文)(北京卷).docx
- 2018年普通高等學(xué)校招生全國(guó)(Ⅱ)統(tǒng)一考試文科數(shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試數(shù) 學(xué)(理)(北京卷).docx
- 2018年普通高等學(xué)校招生全國(guó)統(tǒng)一考試?yán)砜茢?shù)學(xué).docx
- 2018年普通高等學(xué)校招生全國(guó)(Ⅱ)統(tǒng)一考試?yán)砜茢?shù)學(xué).docx
- 2019年全國(guó)統(tǒng)一高考數(shù)學(xué)試卷(理科)(1卷).docx






